
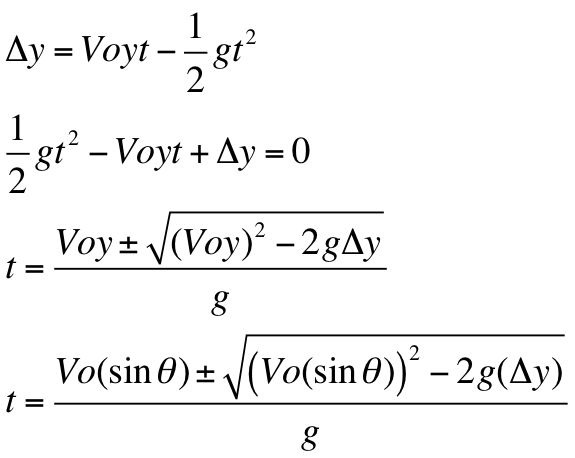
Therefore, the total distance traveled by the projectile during its flight (returning to the same level from which it was launched) is given byĮvaluation of this integral is elementary and can be found in any table of integrals. The element of arc length of a plane curve with equation Which is the equation of a parabola with x intercepts at x = 0 and x = b/a, as shown in Figure 1. The equation of the trajectory reduces to The constants a and b are defined by Equation (6). Trajectory of a projectile in the absence of air resistance. Elimination of t between the equations for x and y results in the equation of the trajectory,įigure 1. In the absence of air resistance, the components of the equation of motion for a projectile launched with an initial speed

But first, we find the average speed, the time-average of instantaneous speed, and the space-average of instantaneous speed for a projectile in the absence of air resistance. In what follows, we show that the space-average of instantaneous speed of a particle is not, in general, equal to its average speed, however, the time-average of instantaneous speed is always equal to the average speed regardless of the nature of the motion. Later on in this article we shall refer to the former average as the space-average of the speed. Whereas the average speed which, by definition is the total distance divided by total time, can be shown to be given by For example, if an object travels half of a distance with speed The average speed of a moving particle is defined as the total distance traveled L divided by the total time T,Īnd the instantaneous speed is defined as magnitude of the instantaneous velocity of the particle at a given time,Ī question that occasionally comes up in discussions related to speed is whether the average of the instantaneous speed of an object during its motion is the same as its average speed. Although this may seem trivial at first sight, it is an important concept in correlating different methods of averaging the speed of an object during its motion as will be explained below. However, to the best of the author’s knowledge and based on extensive literature search, the average speed of a projectile during its motion has not been discussed in the literature at any level. More advanced treatments of the problem include air resistance. Introductory treatment of projectile motion normally ignores air resistance and treats the problem using either differential and integral calculus - or algebra and trigonometry, or even without trigonometry. Projectile motion, one of the simplest examples of two-dimensional motion in classical mechanics, has been extensively studied and thoroughly discussed in the literature and textbooks at different levels. Thus, making it more efficient to calculate one by calculating the other.Īverage Speed, Time-Average, Space-Average, Instantaneous Speed, Projectile Motion, General Motion The equality of average speed and time-average instantaneous speed can be useful in situations where the calculation of one is more difficult than the other. It is then shown that this behavior is shared by general motion of all particles regardless of the dimensionality of motion and the nature of the forces involved. We then show that this quantity is equal to the time-average instantaneous speed of the projectile, but different from its space-average instantaneous speed. We calculate the average speed of a projectile in the absence of air resistance, a quantity that is missing from the treatment of the problem in the literature. Received: JAccepted: JPublished: July 27, 2018
Projectile motion equations without time license#
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0). \begin \Delta y&=-\frac 12\,g\,t^2 \\ -24&=-\frac 12 \,(9.Department of Mathematics and Physics, University of Wisconsin-Parkside, Kenosha, WI, USAĬopyright © 2018 by authors and Scientific Research Publishing Inc. The following equations represent projectile motion in the vertical and horizontal directions. It is characterized by motion in two dimensions and is solely influenced by gravitational force. Projectile motion refers to the motion of any object that is thrown into the air at an angle $\theta$. Through this method, you will gain a better understanding of the equations for projectiles.
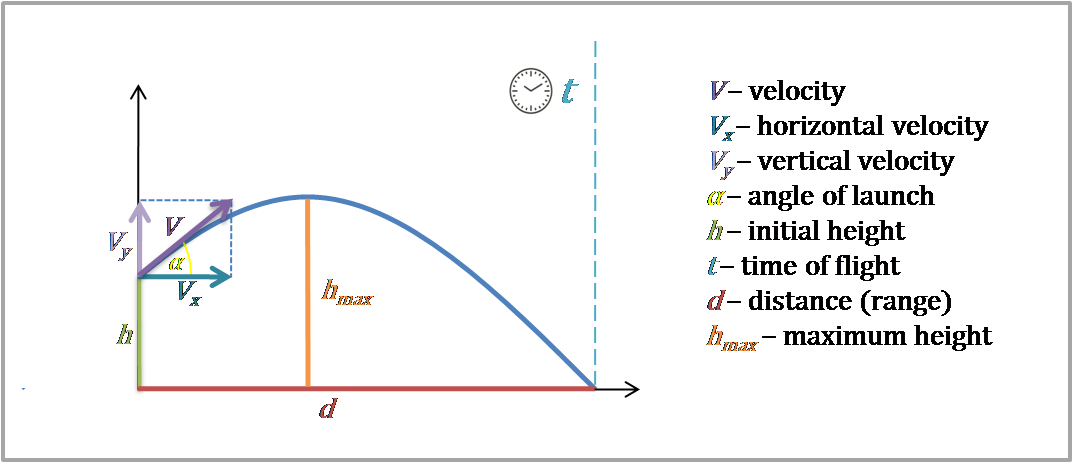
In this article, we have attempted to teach you the formulas for projectile motion by presenting some solved examples.


 0 kommentar(er)
0 kommentar(er)
